Калькулятор тангенс в косинус: Инженерный калькулятор онлайн, Научный калькулятор

Инженерный калькулятор онлайн KALKPRO.RU — самый точный калькулятор корней, степеней, синусов, косинусов, логарифмов!

Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.

Только корректные расчеты по всем правилам математики!

В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.

Всё для вашего удобства:

• быстрые вычисления и загрузка,
• верные расчеты по всем правилам,
• полный функционал,
• понятный интерфейс,
• адаптация под любой размер устройства
• бесплатно
• не надо ничего устанавливать,
• никакой всплывающей назойливой рекламы,
• подробная инструкция с примерами

Содержание справки:

1.  Комплекс операций инженерного калькулятора

2. Инструкция по функциям инженерного калькулятора

3. Как пользоваться инженерным калькулятором – на примерах

4. Тригонометрический калькулятор онлайн — примеры

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов

(n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Инструкция по функциям инженерного калькулятора

Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в

примерах вычислений онлайн. Принцип работы с научным калькулятором такой: вводится число, с которым будет производиться вычисление, затем нажимается кнопка функции или операции, потом, если требуется, то еще цифра, например, степень, в конце — знак равенства. x] – Возведение числа Эйлера в степень

[Frac] – отсекает целую часть, оставляет дробную

[sinh^-1] – обратный гиперболический синус

[sin^-1] – арксинус или обратный синус, arcsin или 1/sin

[deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее

[cosh^-1] — обратный гиперболический косинус

[cos^-1] – аркосинус или обрат. косинус arccos или 1/cos

[2*Pi] – рассчитывает число Пи, помноженное на два

[tanh^-1] – обрат. гиперболический тангенс

[tan^-1] – арктангенс или обратный тангенс, arctg

Как пользоваться MR MC M+ M- MS

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 [x^y] 3 [=]

12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]

Ответ: 1728

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729 [3√x] [=]

729, [³√x] «кубический корень из икс», равенства [=]

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36. y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 [x^y] 6 [=]

Ответ: сорок пять в шестой степ. равно 8303765625

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90 [sin] [=]

Ответ: единица

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60 [cos] [=]

Решение: 0,5

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 [Deg] [=] 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1 [log] [=]

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100 [log] [=]

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой [ln].

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145 [MR]

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

[MR]

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

  

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

Инженерный калькулятор онлайн KALKPRO.RU — самый точный калькулятор корней, степеней, синусов, косинусов, логарифмов!

Почему мы так решили? Наш онлайн калькулятор оперирует числами вплоть до 20 знаков после запятой, в отличие от других. Kalkpro.ru способен точно и достоверно совершить любые вычислительные операции, как простые, так и сложные.

Только корректные расчеты по всем правилам математики!

В любой момент и в любом месте под рукой, универсальный инженерный калькулятор онлайн выполнит для вас любую операцию абсолютно бесплатно, практически мгновенно, просто добавьте программу в закладки.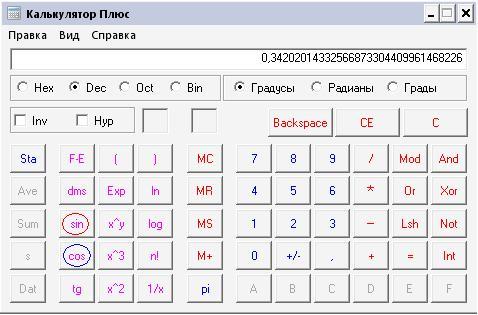

Всё для вашего удобства:

• быстрые вычисления и загрузка,
• верные расчеты по всем правилам,
• полный функционал,
• понятный интерфейс,
• адаптация под любой размер устройства
• бесплатно
• не надо ничего устанавливать,
• никакой всплывающей назойливой рекламы,
• подробная инструкция с примерами

Содержание справки:

1. Комплекс операций инженерного калькулятора

2. Инструкция по функциям инженерного калькулятора

3. Как пользоваться инженерным калькулятором – на примерах

4. Тригонометрический калькулятор онлайн — примеры

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Инструкция по функциям инженерного калькулятора

Для понимания возможностей программы мы даем вам краткую инструкцию, более подробно смотрите в примерах вычислений онлайн. x] – Возведение числа Эйлера в степень

[Frac] – отсекает целую часть, оставляет дробную

[sinh^-1] – обратный гиперболический синус

[sin^-1] – арксинус или обратный синус, arcsin или 1/sin

[deg] – перевод угла в градусах, минутах и секундах в десятичные доли градуса, подробнее

[cosh^-1] — обратный гиперболический косинус

[cos^-1] – аркосинус или обрат. косинус arccos или 1/cos

[2*Pi] – рассчитывает число Пи, помноженное на два

[tanh^-1] – обрат. гиперболический тангенс

[tan^-1] – арктангенс или обратный тангенс, arctg

Как пользоваться MR MC M+ M- MS

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 [x^y] 3 [=]

12, клавиша «икс в степени игрик» [xy], 3, знак равенства [=]

Ответ: 1728

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729 [3√x] [=]

729, [³√x] «кубический корень из икс», равенства [=]

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36. y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 [x^y] 6 [=]

Ответ: сорок пять в шестой степ. равно 8303765625

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами.

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90 [sin] [=]

Ответ: единица

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60 [cos] [=]

Решение: 0,5

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав [Inv], появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

[Deg] позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. [Dms] производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 [Deg] [=] 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 [Dms] [=] 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1 [log] [=]

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100 [log] [=]

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой [ln].

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145 [MR]

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

[MR]

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем [M+], либо [M-] для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой [MR] получится 230, а во втором, после нажатия [M-] и [MR] получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

  

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

Тангенс и котангенс. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти тангенсы и котангенсы угла, представленных как в градусах, так и в радианах. Теоретическую часть и численные примеры смотрите ниже.

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Тангенс и котангенс − теория, примеры и решения

Определение 1. Число, равное отношению

называется тангенсом угла α и обозначается

Определение 2. Число, равное отношению

называется котангенсом угла α и обозначается

Подробнее о синусах и косинусах посмотрите на странице Синус и косинус. Онлайн калькулятор.

Свойство A1. Область определения функции тангенс −это все действительные числа α, удовлетворяющие выражению

где Z множество целых чисел.

Действительно. Из равенства (1) следует, что cos α должен быть отличным от нуля. А это в свою очередь показывает справедливость равенства (3).

Свойство A2. Область определения функции котангенс −это все действительные числа α, удовлетворяющие выражению

где Z множество целых чисел.

Действительно. Из равенства (2) следует, что sin α должен быть отличным от нуля. А это в свою очередь показывает справедливость равенства (4).

Свойство 1. tg α и сtg α нечетные функции, т.е. для любого допустимого значения α справедливы равенства

Доказательство. Воспользуемся равенствами и (cм. на странице Синус и косинус. Онлайн калькулятор). Тогда имеем:

 

Свойство 2. tg α и сtg α периодичные функции с основным периодом π (180°), т.е. для любого допустимого значения α справедливы равенства

или в градусах:

Доказательство. Воспользуемся тем, что или (cм. на странице Синус и косинус. Онлайн калькулятор):

или в градусах:

И вообще

или в градусах:

Использем таблицы синусов и косинусов, и построим таблицу тангенсов и котангенсов некоторых углов, учитывая уравнение (1):

Пример 1. Найти тангенс и котангенс угла равного 420°(или радиан).

Воспользуемся уравнениями (11)− (14):

или :

или :

Пример 2. Найти тангенс и котангенс угла равного -225°(или радиан).

Воспользуемся уравнениями (11)− (14):

или :

или :

Как мы уже знаем из определения синуса и косинуса sin α=y₂, cos α=x₂ (Рис.1). Покажем, что tg α=AN, ctg α=KP

Построим каноническое уравнение прямой, проходящей через точки и (см. статью на странице Каноническое уравнение прямой на плоскости):

Тогда учитывая, что , имеем:

или

Поскольку , , тогда

При x=1 имеем y=tg α. Т.е. tg α − это ординат точки пересечения прямых ON и NA

Выразим в (15) x через y:

Подставляя , , получим:

Взяв y=1, получим x=ctg α. Таким образом ctg α − это абсцисс точки пересечения прямых ON и KP.

Так как для функциий привычнее запись y=f(x), то вместо записей u=tg α и u=сtg α мы будем использовать записи y=tg x и y=сtg x.

График функции тангенс (

y=tg x)

Построим график функции тангенс на интервале . Выберем контрольные точки:

Отметим эти точки на координатной плоскости XOY и проведем через них плавную кривую (Рис. 2)

Учитывая свойство 1 построим симметричную к этой кривой относительно начала координат (Рис.3)

Функция тангенс периодичная (свойство 2) с основным периодом π. Тогда на графике функции тангенс, ветвь на рисунке Рис.2 повторяется бесконечное число раз от -∞ до ∞:

В точках функция имеет разрыв. Каждая прямая вида является вертикальной асимптотой графика функции.

График функции котангенс (

y=сtg x)

Построим график функции котангенс на интервале [0; π). Выберем контрольные точки:

Взяв π≈3, высислим значения x, отметим эти точки на координатной плоскости XOY и проведем через них плавную кривую (Рис. 5)

Функция котангенс периодичная (свойство 2) с основным периодом π. Тогда на графике функции котангенс, ветвь на рисунке Рис.5 повторяется бесконечное число раз от -∞ до ∞:

В точках функция имеет разрыв. Каждая прямая вида является вертикальной асимптотой графика функции котангенс.

Онлайн калькулятор синуса, косинуса, тангенса и котангенса

Калькулятор онлайн вычисляет тригонометрические функции для любого значения угла α заданного в градусах: синус (sin), косинус (cos), тангенс (tg), котангенс (ctg), секанс (sec), косеканс (cosec), версинус (синус-верзус) (versin), коверсинус (косинус-верзус) (vercos), гаверсинус (половина от синус-верзус) (haversin), экссеканс (exsec), экскосеканс (excsc).

Вычислить значения синуса и косинуса для стандартных значений углов можно с помощью тригонометрической окружности (тригонометрического круга)

. Например по тригонометрическому кругу можно найти значение синуса 45 градусов, косинуса 60 градусов или косинуса 90 градусов.

Вычислить значения для тангенсов и котангенсов можно с помощью таблицы синусов, косинусов, тангенсов и котангенсов. Например по таблице тригонометрических функций можно найти значение тангенса 60 градусов или котангенса 30 градусов.

Тригонометрические функций на единичной окружности	Тригонометрический круг (тригонометрическая окружность)

Тригонометрическая таблица основных значений синусов, косинусов, тангенсов и котангенсов.

α

0°

30°

45°

60°

90°

120°

135°

150°

180°

210°

225°

240°

270°

300°

315°

330°

360°

sin(α)

0

1/2

√2/2

√3/2

1

√3/2

√2/2

1/2

0

-1/2

-√2/2

-√3/2

-1

-√3/2

-√2/2

-1/2

0

cos(α)

1

√3/2

√2/2

1/2

0

-1/2

-√2/2

-√3/2

-1

-√3/2

-√2/2

-1/2

0

1/2

√2/2

√3/2

1

tg(α)

0

√3/3

1

√3

—

-√3

-1

-√3/3

0

√3/3

1

√3

—

-√3

-1

-√3/3

0

ctg(α)

—

√3

1

√3/3

0

-√3/3

-1

-√3

—

√3

1

√3/3

0

-√3/3

-1

-√3

—

α

0

π/6

π/4

π/3

π/2

2π/3

3π/4

5π/6

π

7π/6

5π/4

4π/3

3π/2

5π/3

7π/4

11π/6

2π

I. Для справки:

тригонометрические функции

— элементарные функции, которые возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

тригонометрический круг (окружность)

— единичная окружность (круг с радиусом равном единице), с центром в начале системы координат.

Основные тригонометрические функции:

синус угла α

обозначается sin(α) — отношение длины противоположного этому углу катета к гипотенузе;

косинус угла α

обозначается cos(α) — отношение прилежащего этому углу катета к гипотенузе.

Остальные тригонометрические функции можно выразить через синус и косинус:

тангенс

обозначается tg(α) — отношение длины противоположного углу катета к прилежащему катету;

котангенс

обозначается ctg(α) — отношение длины прилежащего к углу катета к противоположному катету;

секанс

обозначается sec(α) — отношение длины гипотенузы к прилежащему к углу катету;

косеканс

обозначается cosec(α) — отношение длины гипотенузы к противоположному катету.

Редко используемые тригонометрические функции:

версинус

обозначается versin(α) — единица минус косинус угла α;

коверсинус

обозначается vercos(α) — единица минус синус угла α;

гаверсинус

обозначается haversin(α) — половина версинуса угла α;

экссеканс

обозначается exsec(α) — секанс угла α минус единица;

экскосеканс

обозначается excsc(α) — косеканс угла α минус единица.

II. Примечание:

1. Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до сотых).
2. Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.

Калькулятор синуса, косинуса, тангенса онлайн

В форме онлайн-калькулятора тригонометрических функций укажите величину угла: число градусов (°), минут (‘), секунд (»). Зная синус, можно найти косинус и тангенс. Если дано дробное значение функции тригонометрии, например, sin=4/5, укажите в поле «числитель» число 4, в поле «знаменатель» число 5. Если tg = -0,5, то число «-0,5» указывается в поле «числитель».
Заполните поле «Текст с картинки». Нажмите кнопку «Решить».

Онлайн калькулятор тригонометрических функций предназначен для того, чтобы быстро найти ответ на задачу, в которой нужно рассчитать, чему равен синус, косинус, тангенс онлайн.

Здесь также выполняется расчет котангенса, секанса, косеканса, версинуса, коверсинуса, гаверсинуса, экссеканса и экскосеканса. Единицы измерения – градусы, минуты, секунды. Ответ вычисляется после нажатия на кнопку «Решить».

Пример задачи. Используем онлайн калькулятор синуса, косинуса, тангенса для того, чтобы найти синус и тангенс, зная косинус угла А в виде дроби Cos A = 1/3. В поле «тригонометрическая функция» указывается «cos», «числитель» — число «1», «знаменатель» — число «3».
Решение синусов и тангенсов:
По таблице «Косинусы» находим значение угла A с градусами и минутами = 70,528779° = 70°32′.
Так как Sin² + Cos² = 1, то, используя тригонометрический калькулятор синусов онлайн:
1) значение синуса Sin A = √1 — (1/3)² = √9/9 — 1/9 = √(9 — 1)/9 = √8/9 = 2,828427 / 3 = 0,942809;
2) значение тангенса tg A = Sin A / Cos A = (2,828427 / 3) • (3/1) = 8,485281/3 = 2,828427.

Пример задачи. Найти синус, тангенс через косинус угла А = Cos A = -0,5 с помощью онлайн калькулятора синусов, косинусов, тангенсов, котангенсов. В поле «тригонометрическая функция» указывается «cos», «числитель» — число «- 0,5».
Решение синусов и тангенсов:
По таблице «Косинусы» находим угол A в градусах = 120° = 120°0′.
Используем формулу основного тригонометрического тождества
Sin² + Cos² = 1. Далее требуется вычислить синус.
1) значение синуса Sin A = √1 — (-0,5)² = √1 — 0,25 = √0,75 = 0,866025;
2) значение тангенса tg A = Sin A / Cos A = 0,866025 / -0,5 = -1,732051.

Пример задачи.
Используем калькулятор синусов и косинусов градусов, минут, секунд онлайн, чтобы найти значение синуса, косинуса, тангенса, котангенса угла A = 12°34’56» = 12 градусов 34 минуты 56 секунд.
Решение:
A = 12°34’56» = 12,582222°
Синус угла sin 12°34’56» = 0,2178404227.
Косинус угла cos 12°34’56» = 0,9759844015.
Тангенс угла tg 12°34’56» = sin 12°34’56» / cos 12°34’56» = 0,2232007218.
Котангенс угла ctg 12°34’56» = cos 12°34’56» / sin 12°34’56» = 4,4802722491.
Секанс sec 12°34’56» = 1 / cos 12°34’56» = 1,0246065402.
Косеканс cosec 12°34’56» = 1 / sin 12°34’56» = 4,5905162484.
Версинус versin 12°34’56» = 1 — cos 12°34’56» = 0,0240155994.

Коверсинус coversin 12°34’56» = 1 — sin 12°34’56» = 0,7821595773.
Гаверсинус haversin 12°34’56» = 0,0240155994 / 2 = 0,0120077997.
Экссеканс exsec 12°34’56» = 1,0246065402 — 1 = 0,0246065402.
Экскосеканс excsc 12°34’56» = 4,5905162484 — 1 = 3,5905162484.

Дано:
ΔABC – прямоугольный треугольник,
гипотенуза AB = c,
катет BC = a,
катет AC = b,

Таблица значений синуса угла

В геометрии синус угла A – отношение противолежащего катета «a» к гипотенузе «c».

Математическая формула синуса. sin A = a/c

Синус угла 0 градусов: sin 0° = sin 0 = 0

Синус угла 30 градусов: sin 30° = sin (π/6) = 1/2

Синус угла 45 градусов: sin 45° = sin (π/4) = √2/2

Синус угла 60 градусов: sin 60° = sin (π/3) = √3/2

Синус угла 90 градусов: sin 90° = sin (π/2) = 1

Синус угла 180 градусов: sin 180° = 0

Таблица косинуса угла

Косинус угла A – отношение прилежащего катета «b» к гипотенузе «c».

Формула косинуса. cos A = b/c

Косинус угла 0 градусов: cos 0° = cos 0 = 1

Косинус угла 30 градусов: cos 30° = cos (π/6) = √3/2

Косинус угла 45 градусов: cos 45° = cos (π/4) = √2/2

Косинус угла 60 градусов: cos 60° = cos (π/3) = 1/2

Косинус угла 90 градусов: cos 90° = cos (π/2) = 0

Косинус угла 180 градусов: cos 180° = –1

Таблица тангенса угла

В тригонометрии тангенс угла A – отношение противолежащего катета «a» к прилежащему катету «b».

Геометрическая формула тангенса. tg A = a/b

Тангенс угла 0 градусов: tg 0° = tg 0 = 0

Тангенс угла 30 градусов: tg 30° = tg (π/6) = √3/3

Тангенс угла 45 градусов: tg 45° = tg (π/4) = 1

Тангенс угла 60 градусов: tg 60° = tg (π/3) = √3

Тангенс угла 90 градусов: tg 90° = tg (π/2) = не определяется

Тангенс угла 180 градусов: tg 180° = 0

Котангенс угла

Котангенс угла A – отношение длины прилежащего катета «b» к противолежащему катету «a».

Формула котангенса. ctg A = b/a

Секанс

Секанс угла A равен отношению гипотенузы «c» к длине прилежащего катета «b».

Формула секанса. sec A = c/b

Косеканс

Косеканс угла A – отношение гипотенузы «c» к противолежащему катету «a».

Формула косеканса. cosec A = c/a

Версинус

Формула версинуса. versin A = 1 — cos A.

Коверсинус

Коверсинус рассчитывается как coversin A = 1 — sin A.

Гаверсинус

Формула гаверсинуса. haversin A = (versin A)/2.

Экссеканс

Экссеканс вычисляется по формуле: exsec A = sec A — 1.

Экскосеканс

Формула экскосеканса. excsc A = cosec A — 1.

Найти синус, косинус, тангенс онлайн: формулы тригонометрических функций

В калькуляторе тригонометрических функций укажите параметры угла:
градусов (°), минут (‘), секунд (»).
Если дано значение синуса, косинуса или тангенса, то следует выбрать функцию в списке — sin, cos или tg — и в поле «для числителя» указать это значение (например, 0,2 или 0,12345). При этом все остальные поля остаются пустыми.
Если известно дробное значение функции, то числитель дроби указать в поле «для числителя», знаменатель — в поле «знаменатель дробного значения». Например, если синус равен 3/5, то выбрать в списке «sin», в поле «для числителя» указать цифру 3, в поле «знаменатель дробного значения» — цифру 5.
Заполните поле «Текст». Нажмите кнопку «Решить».

При помощи данного онлайн-калькулятора тригонометрических функций можно вычислить, чему равен синус, косинус, тангенс, котангенс, секанс, косеканс, версинус, коверсинус, гаверсинус, экссеканс, экскосеканс угла, зная, сколько составляет угол в двух единицах измерения – градусах и минутах. Результат задачи вычисляет компьютерная программа.

Дано:
ΔABC – прямоугольный треугольник,
гипотенуза AB = c,
катет BC = a,
катет AC = b,

Таблица значений синуса угла

В тригонометрии синус угла A – отношение противолежащего катета a к гипотенузе c.

Формула синуса. sin A = a / c

Синус угла 0 градусов: sin 0° = sin 0 = 0

Синус угла 30 градусов: sin 30° = sin (π/6) = 1/2

Синус угла 45 градусов: sin 45° = sin (π/4) = √2/2

Синус угла 60 градусов: sin 60° = sin (π/3) = √3/2

Синус угла 90 градусов: sin 90° = sin (π/2) = 1

Синус угла 180 градусов: sin 180° = 0

Косинус угла.

Таблица

Косинус угла A – отношение прилежащего катета b к гипотенузе c.

Математическая формула косинуса. cos A = b / c

Косинус угла 0 градусов: cos 0° = cos 0 = 1

Косинус угла 30 градусов: cos 30° = cos (π/6) = √3/2

Косинус угла 45 градусов: cos 45° = cos (π/4) =√2/2

Косинус угла 60 градусов: cos 60° = cos (π/3) =
1/2

Косинус угла 90 градусов: cos 90° = cos (π/2) = 0

Косинус угла 180 градусов: cos 180° = –1

Тангенс угла. Таблица

В геометрии тангенс угла A – отношение противолежащего катета a к прилежащему катету b.

Геометрическая формула тангенса. tg A = a / b

Тангенс угла 0 градусов: tg 0° = tg 0 = 0

Тангенс угла 30 градусов: tg 30° = tg(π/6) =√3/3

Тангенс угла 45 градусов: tg 45° = tg(π/4) = 1

Тангенс угла 60 градусов: tg 60° = tg(π/3) = √3

Тангенс угла 90 градусов: tg 90° = tg(π/2) = не определяется

Тангенс угла 180 градусов: tg 180° = 0

Котангенс угла

Котангенс угла A – отношение длины прилежащего катета b к противолежащему катету a.

Формула котангенса. ctg A = b / a

Секанс

Секанс угла A равен отношению гипотенузы c к длине прилежащего катета b.

Формула секанса. sec A = c / b

Косеканс

Косеканс угла A – отношение гипотенузы c к противолежащему катету a.

Формула косеканса. cosec A = c / a

Версинус

Формула версинуса. versin A = 1 — cos A.

Коверсинус

Коверсинус определяется как coversin A = 1 — sin A.

Гаверсинус

Формула гаверсинуса. haversin A = (versin A) / 2.

Экссеканс

Экссеканс определяется по формуле: exsec A = sec A — 1.

Экскосеканс

Формула экскосеканса. excsc A = cosec A — 1.

Таблица синусов и косинусов. Онлайн-калькулятор

В данной таблице приведены значения синусов и косинусов для углов от 0 до 359 градусов. Чтобы рассчитать значения тригонометрических функций для более точных углов (с минутами и секундами) или углов больше 360 градусов или углов с отрицательными значениями (например 8° 5′ 53″ или -1775° 15′ 22″ ) можно воспользоваться калькулятором синусов и косинусов.
Примечание: в калькуляторе этот знак означает, что можно поставить отрицательное значение угла. При нажатии на этот знак минус появится, при повторном нажатии исчезнет.

Таблица углов от 0 до 179 градусов

Угол (градусы)	Синус (Sin)	Косинус (Cos)
0	0	1
1	0.01745241	0.9998477
2	0.0348995	0.99939083
3	0.05233596	0.99862953
4	0.06975647	0.99756405
5	0.08715574	0.9961947
6	0.10452846	0.9945219
7	0.12186934	0.99254615
8	0.1391731	0.99026807
9	0.15643447	0.98768834
10	0.17364818	0.98480775
11	0.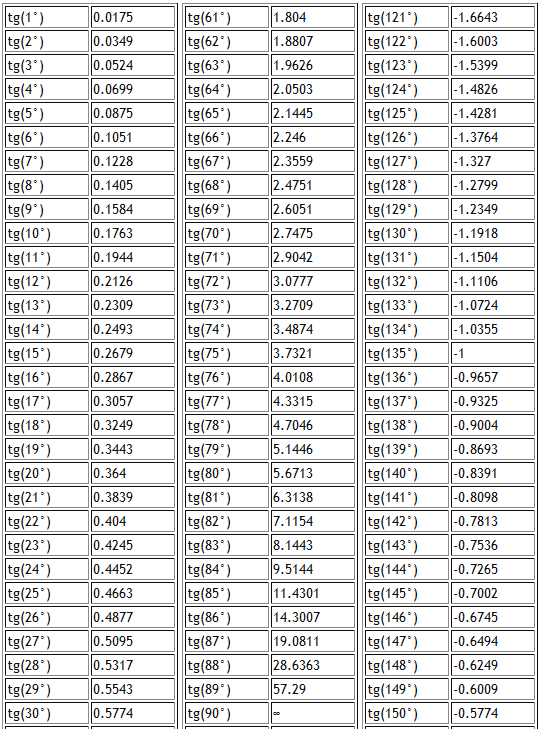 190809	0.98162718
12	0.20791169	0.9781476
13	0.22495105	0.97437006
14	0.2419219	0.97029573
15	0.25881905	0.96592583
16	0.27563736	0.9612617
17	0.2923717	0.95630476
18	0.30901699	0.95105652
19	0.32556815	0.94551858
20	0.34202014	0.93969262
21	0.35836795	0.93358043
22	0.37460659	0.92718385
23	0.39073113	0.92050485
24	0.40673664	0.91354546
25	0.42261826	0.90630779
26	0.43837115	0.89879405
27	0.4539905	0.89100652
28	0.46947156	0.88294759
29	0.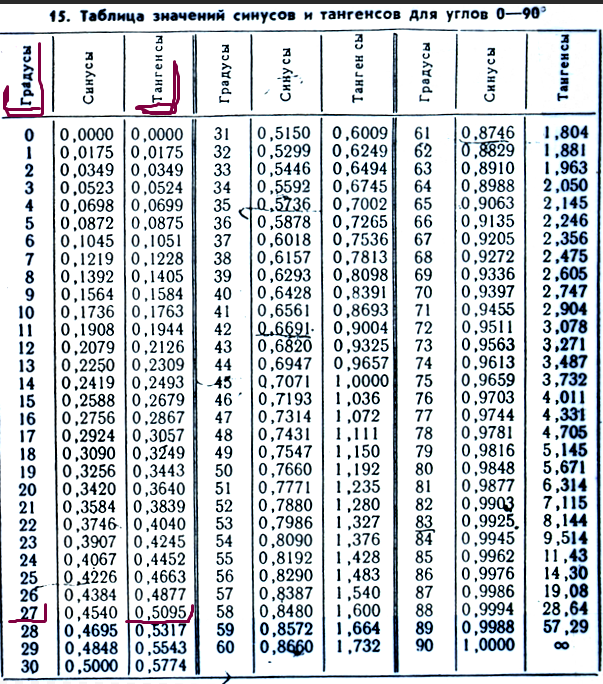 48480962	0.87461971
30	0.5	0.8660254
31	0.51503807	0.8571673
32	0.52991926	0.8480481
33	0.54463904	0.83867057
34	0.5591929	0.82903757
35	0.57357644	0.81915204
36	0.58778525	0.80901699
37	0.60181502	0.79863551
38	0.61566148	0.78801075
39	0.62932039	0.77714596
40	0.64278761	0.76604444
41	0.65605903	0.75470958
42	0.66913061	0.74314483
43	0.68199836	0.7313537
44	0.69465837	0.7193398
45	0.70710678	0.70710678
46	0.7193398	0.69465837
47	0. 7313537	0.68199836
48	0.74314483	0.66913061
49	0.75470958	0.65605903
50	0.76604444	0.64278761
51	0.77714596	0.62932039
52	0.78801075	0.61566148
53	0.79863551	0.60181502
54	0.80901699	0.58778525
55	0.81915204	0.57357644
56	0.82903757	0.5591929
57	0.83867057	0.54463904
58	0.8480481	0.52991926
59	0.8571673	0.51503807
60	0.8660254	0.5
61	0.87461971	0.48480962
62	0.88294759	0.46947156
63	0.89100652	0.4539905
64	0.89879405	0.43837115
65	0. 90630779	0.42261826
66	0.91354546	0.40673664
67	0.92050485	0.39073113
68	0.92718385	0.37460659
69	0.93358043	0.35836795
70	0.93969262	0.34202014
71	0.94551858	0.32556815
72	0.95105652	0.30901699
73	0.95630476	0.2923717
74	0.9612617	0.27563736
75	0.96592583	0.25881905
76	0.97029573	0.2419219
77	0.97437006	0.22495105
78	0.9781476	0.20791169
79	0.98162718	0.190809
80	0.98480775	0.17364818
81	0.98768834	0.15643447
82	0.99026807	0.1391731
83	0. 99254615	0.12186934
84	0.9945219	0.10452846
85	0.9961947	0.08715574
86	0.99756405	0.06975647
87	0.99862953	0.05233596
88	0.99939083	0.0348995
89	0.9998477	0.01745241
90	1	0
91	0.9998477	-0.01745241
92	0.99939083	-0.0348995
93	0.99862953	-0.05233596
94	0.99756405	-0.06975647
95	0.9961947	-0.08715574
96	0.9945219	-0.10452846
97	0.99254615	-0.12186934
98	0.99026807	-0.1391731
99	0.98768834	-0.15643447
100	0.98480775	-0.17364818
101	0. 98162718	-0.190809
102	0.9781476	-0.20791169
103	0.97437006	-0.22495105
104	0.97029573	-0.2419219
105	0.96592583	-0.25881905
106	0.9612617	-0.27563736
107	0.95630476	-0.2923717
108	0.95105652	-0.30901699
109	0.94551858	-0.32556815
110	0.93969262	-0.34202014
111	0.93358043	-0.35836795
112	0.92718385	-0.37460659
113	0.92050485	-0.39073113
114	0.91354546	-0.40673664
115	0.90630779	-0.42261826
116	0.89879405	-0.43837115
117	0.89100652	-0.4539905
118	0. 88294759	-0.46947156
119	0.87461971	-0.48480962
120	0.8660254	-0.5
121	0.8571673	-0.51503807
122	0.8480481	-0.52991926
123	0.83867057	-0.54463904
124	0.82903757	-0.5591929
125	0.81915204	-0.57357644
126	0.80901699	-0.58778525
127	0.79863551	-0.60181502
128	0.78801075	-0.61566148
129	0.77714596	-0.62932039
130	0.76604444	-0.64278761
131	0.75470958	-0.65605903
132	0.74314483	-0.66913061
133	0.7313537	-0.68199836
134	0.7193398	-0.69465837
135	0. 70710678	-0.70710678
136	0.69465837	-0.7193398
137	0.68199836	-0.7313537
138	0.66913061	-0.74314483
139	0.65605903	-0.75470958
140	0.64278761	-0.76604444
141	0.62932039	-0.77714596
142	0.61566148	-0.78801075
143	0.60181502	-0.79863551
144	0.58778525	-0.80901699
145	0.57357644	-0.81915204
146	0.5591929	-0.82903757
147	0.54463904	-0.83867057
148	0.52991926	-0.8480481
149	0.51503807	-0.8571673
150	0.5	-0.8660254
151	0.48480962	-0.87461971
152	0. 46947156	-0.88294759
153	0.4539905	-0.89100652
154	0.43837115	-0.89879405
155	0.42261826	-0.90630779
156	0.40673664	-0.91354546
157	0.39073113	-0.92050485
158	0.37460659	-0.92718385
159	0.35836795	-0.93358043
160	0.34202014	-0.93969262
161	0.32556815	-0.94551858
162	0.30901699	-0.95105652
163	0.2923717	-0.95630476
164	0.27563736	-0.9612617
165	0.25881905	-0.96592583
166	0.2419219	-0.97029573
167	0.22495105	-0.97437006
168	0.20791169	-0.9781476
169	0. 190809	-0.98162718
170	0.17364818	-0.98480775
171	0.15643447	-0.98768834
172	0.1391731	-0.99026807
173	0.12186934	-0.99254615
174	0.10452846	-0.9945219
175	0.08715574	-0.9961947
176	0.06975647	-0.99756405
177	0.05233596	-0.99862953
178	0.0348995	-0.99939083
179	0.01745241	-0.9998477

Таблица углов от 180 до 359 градусов

Угол (градусы)	Синус (Sin)	Косинус (Cos)
180	0	-1
181	-0.01745241	-0.9998477
182	-0.0348995	-0.99939083
183	-0. 05233596	-0.99862953
184	-0.06975647	-0.99756405
185	-0.08715574	-0.9961947
186	-0.10452846	-0.9945219
187	-0.12186934	-0.99254615
188	-0.1391731	-0.99026807
189	-0.15643447	-0.98768834
190	-0.17364818	-0.98480775
191	-0.190809	-0.98162718
192	-0.20791169	-0.9781476
193	-0.22495105	-0.97437006
194	-0.2419219	-0.97029573
195	-0.25881905	-0.96592583
196	-0.27563736	-0.9612617
197	-0.2923717	-0.95630476
198	-0.30901699	-0.95105652
199	-0.32556815	-0.94551858
200	-0. 34202014	-0.93969262
201	-0.35836795	-0.93358043
202	-0.37460659	-0.92718385
203	-0.39073113	-0.92050485
204	-0.40673664	-0.91354546
205	-0.42261826	-0.90630779
206	-0.43837115	-0.89879405
207	-0.4539905	-0.89100652
208	-0.46947156	-0.88294759
209	-0.48480962	-0.87461971
210	-0.5	-0.8660254
211	-0.51503807	-0.8571673
212	-0.52991926	-0.8480481
213	-0.54463904	-0.83867057
214	-0.5591929	-0.82903757
215	-0.57357644	-0.81915204
216	-0.58778525	-0.80901699
217	-0. 60181502	-0.79863551
218	-0.61566148	-0.78801075
219	-0.62932039	-0.77714596
220	-0.64278761	-0.76604444
221	-0.65605903	-0.75470958
222	-0.66913061	-0.74314483
223	-0.68199836	-0.7313537
224	-0.69465837	-0.7193398
225	-0.70710678	-0.70710678
226	-0.7193398	-0.69465837
227	-0.7313537	-0.68199836
228	-0.74314483	-0.66913061
229	-0.75470958	-0.65605903
230	-0.76604444	-0.64278761
231	-0.77714596	-0.62932039
232	-0.78801075	-0.61566148
233	-0.79863551	-0.60181502
234	-0. 80901699	-0.58778525
235	-0.81915204	-0.57357644
236	-0.82903757	-0.5591929
237	-0.83867057	-0.54463904
238	-0.8480481	-0.52991926
239	-0.8571673	-0.51503807
240	-0.8660254	-0.5
241	-0.87461971	-0.48480962
242	-0.88294759	-0.46947156
243	-0.89100652	-0.4539905
244	-0.89879405	-0.43837115
245	-0.90630779	-0.42261826
246	-0.91354546	-0.40673664
247	-0.92050485	-0.39073113
248	-0.92718385	-0.37460659
249	-0.93358043	-0.35836795
250	-0.93969262	-0.34202014
251	-0. 94551858	-0.32556815
252	-0.95105652	-0.30901699
253	-0.95630476	-0.2923717
254	-0.9612617	-0.27563736
255	-0.96592583	-0.25881905
256	-0.97029573	-0.2419219
257	-0.97437006	-0.22495105
258	-0.9781476	-0.20791169
259	-0.98162718	-0.190809
260	-0.98480775	-0.17364818
261	-0.98768834	-0.15643447
262	-0.99026807	-0.1391731
263	-0.99254615	-0.12186934
264	-0.9945219	-0.10452846
265	-0.9961947	-0.08715574
266	-0.99756405	-0.06975647
267	-0.99862953	-0.05233596
268	-0. 99939083	-0.0348995
269	-0.9998477	-0.01745241
270	-1	0
271	-0.9998477	0.01745241
272	-0.99939083	0.0348995
273	-0.99862953	0.05233596
274	-0.99756405	0.06975647
275	-0.9961947	0.08715574
276	-0.9945219	0.10452846
277	-0.99254615	0.12186934
278	-0.99026807	0.1391731
279	-0.98768834	0.15643447
280	-0.98480775	0.17364818
281	-0.98162718	0.190809
282	-0.9781476	0.20791169
283	-0.97437006	0.22495105
284	-0.97029573	0.2419219
285	-0.96592583	0.25881905
286	-0.9612617	0.27563736
287	-0.95630476	0.2923717
288	-0.95105652	0.30901699
289	-0.94551858	0.32556815
290	-0.93969262	0.34202014
291	-0.93358043	0.35836795
292	-0.92718385	0.37460659
293	-0.92050485	0.39073113
294	-0.91354546	0.40673664
295	-0.90630779	0.42261826
296	-0.89879405	0.43837115
297	-0.89100652	0.4539905
298	-0.88294759	0.46947156
299	-0.87461971	0.48480962
300	-0.8660254	0.5
301	-0.8571673	0.51503807
302	-0.8480481	0.52991926
303	-0.83867057	0.54463904
304	-0.82903757	0.5591929
305	-0.81915204	0.57357644
306	-0.80901699	0.58778525
307	-0.79863551	0.60181502
308	-0.78801075	0.61566148
309	-0.77714596	0.62932039
310	-0.76604444	0.64278761
311	-0.75470958	0.65605903
312	-0.74314483	0.66913061
313	-0.7313537	0.68199836
314	-0.7193398	0.69465837
315	-0.70710678	0.70710678
316	-0.69465837	0.7193398
317	-0.68199836	0.7313537
318	-0.66913061	0.74314483
319	-0.65605903	0.75470958
320	-0.64278761	0.76604444
321	-0.62932039	0.77714596
322	-0.61566148	0.78801075
323	-0.60181502	0.79863551
324	-0.58778525	0.80901699
325	-0.57357644	0.81915204
326	-0.5591929	0.82903757
327	-0.54463904	0.83867057
328	-0.52991926	0.8480481
329	-0.51503807	0.8571673
330	-0.5	0.8660254
331	-0.48480962	0.87461971
332	-0.46947156	0.88294759
333	-0.4539905	0.89100652
334	-0.43837115	0.89879405
335	-0.42261826	0.90630779
336	-0.40673664	0.91354546
337	-0.39073113	0.92050485
338	-0.37460659	0.92718385
339	-0.35836795	0.93358043
340	-0.34202014	0.93969262
341	-0.32556815	0.94551858
342	-0.30901699	0.95105652
343	-0.2923717	0.95630476
344	-0.27563736	0.9612617
345	-0.25881905	0.96592583
346	-0.2419219	0.97029573
347	-0.22495105	0.97437006
348	-0.20791169	0.9781476
349	-0.190809	0.98162718
350	-0.17364818	0.98480775
351	-0.15643447	0.98768834
352	-0.1391731	0.99026807
353	-0.12186934	0.99254615
354	-0.10452846	0.9945219
355	-0.08715574	0.9961947
356	-0.06975647	0.99756405
357	-0.05233596	0.99862953
358	-0.0348995	0.99939083
359	-0.01745241	0.9998477

Калькулятор синусов и косинусов

Рассчитать

Исходный угол: 180° 20′ 54″
Расчетный угол в градусах: 180.34833333333°

Синус (sin) = -0.006079526
Косинус (cos) = -0.999981520
Тангенс (tg) = 0.006079638
Котангенс (ctg) = 164.483467955

Поделитесь информацией с друзьями

Другие таблицы

Таблица тангенсов и котангенсов
Таблица кубов натуральных чисел
Тренажер таблицы умножения

Калькулятор тригонометрии

. Простой способ найти sin, cos, tan, cot

Этот калькулятор тригонометрии поможет вам в двух популярных случаях, когда необходима тригонометрия. Если вы хотите найти значения синуса, косинуса, тангенса и их обратных функций, используйте первую часть калькулятора. Ищете недостающую сторону или угол в прямоугольном треугольнике с помощью тригонометрии? Наш инструмент — тоже беспроигрышный вариант! Введите 2–3 заданных значения во второй части калькулятора, и вы в мгновение ока найдете ответ.Прокрутите вниз, если хотите узнать больше о тригонометрии и о том, где ее можно применить.

Есть много других инструментов, полезных при решении задач тригонометрии. Ознакомьтесь с двумя популярными тригонометрическими законами: калькуляторами закона синусов и закона косинусов, которые помогают решить любой тип треугольника. Если вы хотите узнать больше о тригонометрических функциях, перейдите к нашим специальным инструментам:

Что такое тригонометрия?

Тригонометрия — это раздел математики. Само это слово происходит от греческого слова trignon (что означает «треугольник») и metron («мера»).Как следует из названия, тригонометрия имеет дело в основном с углами и треугольниками ; в частности, он определяет и использует отношения и соотношения между углами и сторонами в треугольниках. Таким образом, основное приложение — решение треугольников, в частности прямоугольных, а также любого другого типа треугольника, который вам нравится.

Тригонометрия имеет множество приложений: от повседневных задач, таких как вычисление высоты или расстояния между объектами, до спутниковой навигационной системы, астрономии и географии.Кроме того, функции синуса и косинуса являются фундаментальными для описания периодических явлений — благодаря им мы можем описывать колебательные движения (как простой маятник) и волны, такие как звук, вибрация или свет.

Тригонометрия и тригонометрические функции используются во многих различных областях науки и техники, если упомянуть лишь некоторые из них: музыка, акустика, электроника, медицина и медицинская визуализация, биология, химия, метеорология, электротехника, машиностроение и гражданское строительство, даже экономика. Тригонометрические функции действительно все вокруг нас!

Калькулятор триггеров нахождение sin, cos, tan, cot, sec, csc

Чтобы найти тригонометрические функции угла, введите выбранный угол в градусах или радианах.Под калькулятором появятся шесть самых популярных триггерных функций — три основных: синус, косинус и тангенс, а также их обратные величины: косеканс, секанс и котангенс. Кроме того, если угол острый, будет отображаться прямоугольный треугольник, который может помочь вам понять, как могут быть интерпретированы функции.

Чтобы найти недостающие стороны или углы прямоугольного треугольника, все, что вам нужно сделать, это ввести известные переменные в калькулятор тригонометрии. Вам нужны только два заданных значения в случае:

• односторонний и односторонний
• с двух сторон
• площадь и одна сторона

Помните, что если вы знаете два угла, этого недостаточно, чтобы найти стороны треугольника.Два треугольника, имеющие одинаковую форму (что означает, что они имеют равные углы), могут быть разных размеров (не с одинаковой длиной стороны) — такая взаимосвязь называется сходством треугольников . Если стороны имеют одинаковую длину, то треугольники равны и соответствуют .

Что такое тригонометрия?

Тригонометрия — это исследование отношений внутри треугольника . Для прямоугольных треугольников соотношение между любыми двумя сторонами всегда одинаково и задается в виде тригонометрических соотношений, cos, sin и tan.Тригонометрия также может помочь найти некоторую недостающую информацию о треугольнике , например, правило синуса.

Сложна ли тригонометрия?

Поначалу тригонометрия может быть сложной задачей, но после некоторой практики вы ее освоите! Вот несколько советов по тригонометрии: Обозначьте гипотенузу, смежную и противоположную на вашем треугольнике, чтобы помочь вам выяснить, какую идентификацию использовать, и запомните мнемонику SOHCAHTOA для тригонометрических отношений!

Для чего используется тригонометрия?

Тригонометрия используется для поиска информации обо всех треугольниках и, в частности, прямоугольных треугольниках.Поскольку треугольников повсюду в природе , тригонометрия используется вне математики, в таких областях, как строительство, физика, химическая инженерия и астрономия.

Кто изобрел тригонометрию?

Поскольку тригонометрия — это взаимосвязь между углами и сторонами треугольника, никто не придумал ее , она все равно была бы там, даже если бы об этом никто не знал! Первыми, кто открыл часть тригонометрии, были древние египтяне и вавилоняне , но Евклид и Архемид первыми подтвердили идентичность, хотя они сделали это с помощью форм, а не алгебры.

Какой уровень у тригонометрии?

Тригонометрия — это , которые обычно преподают подросткам в возрасте 13-15 лет , что составляет классов 8 и 9 в США и лет 9 и 10 в Великобритании. Точный возраст преподавания тригонометрии зависит от страны, школы и способностей учеников.

Касательная. Калькулятор tan (x) | Определение

Этот калькулятор тангенса поможет вам найти тангенс любого угла, который вы хотите. Просто введите угол в градусах или радианах, и тангенс появится в мгновение ока.Если вы хотите понять, что такое касательная, вам интересно определение касательной или вывод формулы касательной, продолжайте читать! Также там вас ждет sin over cos meme.

Что такое касательная? Определение касательной, формула касательной

Касательная — одна из трех наиболее распространенных тригонометрических функций (наряду с синусом и косинусом). Его можно определить как

соотношение сторон: противоположной и прилегающей к углу, в прямоугольном треугольнике.

НО! Есть еще одна геометрическая концепция, называемая , касательная . Это линия или плоскость, которая касается кривой или криволинейной поверхности в какой-то точке, но при удлинении не пересекает ее в этой точке.

Слово касательная происходит от латинского tangere , что означает «касаться». И имя нашей тригонометрической функции также происходит от этого значения! Посмотрите на картинку ниже:

Нарисуйте единичный круг. Точка C — это пересечение прямой, содержащей радиус, и прямой x = 1.Тогда tan (α) — это просто координата y точки C.

Tangent — sin over cos

Тангенс угла можно также определить как его синус, деленный на косинус. Но почему это так? Взгляните на изображение единичного круга, и все должно быть ясно:

Зная определение синуса — напротив гипотенузы — мы можем узнать, что для прямоугольного треугольника из изображения sin (α) = y . Аналогично, косинус может быть определен как , смежный по гипотенузе , поэтому в нашем случае он равен x.Затем, в предыдущем абзаце, вы узнали, что касательная равна напротив соседней стороны . Итак, для нашего примера tan (α) = y / x, и это можно заменить синусом и косинусом нашего угла интереса, чтобы получить окончательную формулу:

tan (α) = sin (α) / cos (α)

Не так давно в Интернете можно было найти математические анекдоты — sin over cos memes . Мы уверены, что, прочитав этот абзац, вы получите его!

А как насчет загар герина 🍊? Tan go 🎶? Ti tan ic 🚢? Или даже sa tan ism? Подумайте, какие еще слова могли бы сделать такой ребус!

Закон касательных

Закон касательных описывает соотношение между тангенсом двух углов треугольника и длинами противоположных сторон.В частности, в нем говорится, что:

(a - b) / (a ​​+ b) = tan (0,5 (α - β)) / tan (0,5 (α + β))

Хотя закон касательных не так популярен, как закон синусов или закон косинусов, он может оказаться полезным, если мы дали:

• две стороны и угол между ними;
• два угла и бортик.

Калькулятор тангенса — пример использования

Все, что вам нужно сделать, это ввести одно значение в калькулятор — угол в радианах или градусах.Чтобы переключаться между единицами измерения, нажмите на название единицы и выберите из раскрывающегося списка. Тогда вы сразу увидите результат — значение тангенса угла интереса. Помните, что tan может быть неопределенным . Эта ситуация возникает, когда cos (α) равен 0, потому что мы никогда не можем разделить на ноль (другое объяснение: линии будут параллельны, поэтому они никогда не пересекаются друг с другом и не образуют точку C).

Косинус. Калькулятор | Определение | График

Калькулятор косинусов является двойным инструментом нашего калькулятора синусов. Добавьте к ним инструмент касательной, и вы получите набор самых популярных тригонометрических функций.Просто введите угол — в градусах или радианах — и вы сразу же найдете значение косинуса. Читайте дальше, чтобы понять , что такое косинус и найти определение косинуса , а также аккуратную таблицу со значениями косинуса для основных углов, таких как cos 0 °, cos 30 ° или cos 45 °.

Что такое косинус? Определение косинуса

Косинус — одна из самых основных тригонометрических функций. Его можно определить на основе прямоугольного треугольника или единичного круга, аналогично определению синуса:

Косинус угла — это длина соседней стороны, деленная на длину гипотенузы .

cos (α) = смежный / гипотенуза = b / c

Если вы не уверены, что такое рядом с и гипотенуза (а также напротив ), посмотрите объяснение в калькуляторе синусов.

Название косинус происходит от латинского префикса co- и синусоидальной функции — так что это буквально означает дополнение синуса . И действительно, функция косинуса может быть определена таким образом: как синус дополнительного угла — другого непрямого угла.Сокращение косинуса — cos , например cos (30 °) .

Важные свойства функции косинуса:

• Диапазон (область значений) косинуса -1 ≤ cos (α) ≤ 1
• Косинус периода равен 2π
• Это четная функция (а синус нечетный!), Что означает, что cos (-α) = cos (α)
• Определение косинуса необходимо для понимания закона косинусов — очень полезного закона для решения любого треугольника.

График и таблица косинусов (cos 0, cos 30 градусов, cos 45 градусов …)

На изображении ниже показана функция косинуса в диапазоне <-2π, 2π>:

Точное значение косинуса особенно легко запомнить и определить для определенных углов — вероятно, вы узнали, что cos 0 ° = 1, cos 30 ° = √3 / 2 или cos 45 ° = √2 / 2. Остальные основные углы указаны в таблице:

CSV в HTML с использованием codebeautify.org

α (угол)		грех (α)
градусов	Радианы	точно	десятичный
0 °	0	1	1
15 °	π / 12	(√6 + √2) / 4	0.9659258263
30 °	π / 6	√3 / 2	0,8660254038
45 °	π / 4	√2 / 2	0,7071067812
60 °	π / 3	0.5	0,5
75 °	5π / 12	(√6 — √2) / 4	0,25881
90 °	π / 2	0	0
105 °	7π / 12	— (√6 — √2) / 4	-0.25881
120 °	2π / 3	-0,5	-0,5
135 °	3π / 4	-√2 / 2	-0,7071067812
150 °	5π / 6	-√3 / 2	-0.8660254038
165 °	11π / 12	— (√6 + √2) / 4	-0,9659258263
180 °	π	-1	-1

Кроме того, вы можете наблюдать, как функция косинуса ведет себя в соответствии с квадрантом, в котором она находится.Помните о периодичности функции косинуса cos (α + 360 °) = cos (α) , если ваш угол выходит за пределы диапазона, указанного в таблице ниже.

Квадрант / граница	градусов	Радианы	Значение	Знак	Однообразие	Выпуклость
	0 °	0	1		максимум
1-й квадрант	0 ° <α <90 °	0 <α <π / 2	0	+	убывающая	вогнутый
	90 °	π / 2	0		корень, перегиб
2-й квадрант	90 ° <α <180 °	π / 2 <α <π	-1	–	убывающая	выпуклый
	180 °	π	-1		минимум
3-й квадрант	180 ° <α <270 °	π <α <3π / 2	-1 <грех (α) <0	–	увеличение	выпуклый
	270 °	3π / 2	0		корень, перегиб
4-й квадрант	270 ° <α <360 °	3π / 2 <α <2π	0 <грех (α) <1	+	увеличение	вогнутый

Пример: как использовать калькулятор косинусов

Теперь вы знаете, что такое косинус, использовать этот калькулятор косинуса совсем несложно!

1. Введите угол .Переключайтесь между единицами простым щелчком по названию единицы. Возьмем для примера 40 °.
2. Сохраняйте спокойствие и прочтите результат — в нашем случае cos (40 °) ≈ 0,766 (помните, это приблизительное, точное значение косинуса можно найти только для определенных случаев).

Попробуйте этот калькулятор косинусов! Поиграйте, набрав значение косинуса и найдя угол. Единственное, на что следует обратить внимание, это то, что наш инструмент покажет вам углы в диапазоне от 0 до 180 ° — поскольку вы знаете о периодичности и о том, что косинус является четной функцией, вам не составит труда найти другие возможные решения. .

Калькулятор Arcsin. Нахождение обратной функции синуса.

С помощью этого калькулятора арксинуса (или калькулятора обратного синуса) у вас не будет проблем с поиском арксинуса в вашей задаче. Просто введите значение синуса для треугольника, и появится нужный угол. Единственное, что вам нужно запомнить, это ограниченная область арксинуса (−1 ≤ sine ≤ 1). Если вам интересно, , что такое арксинус или , как выглядит график arcsin x , не ждите больше — прокрутите вниз, и вы найдете ответы ниже! Мы также включили короткий абзац об отношениях арксинусов, таких как отношения между интегралом арксинуса и производной.И так, чего же ты ждешь?

Что такое арксинус?

Арксинус — это функция, обратная синусоиде. Другими словами, это помогает найти угол треугольника, который имеет известное значение синуса. Поскольку область синуса для действительных чисел равна [-1, 1], мы можем вычислить арксинус только для чисел в этом интервале.

Синус — периодическая функция, поэтому существует несколько чисел, которые имеют одинаковое значение синуса. Например, sin (0) = 0, но также sin (π) = 0, sin (2π) = 0, sin (-π) = 0 и sin (-326π) = 0.Следовательно, если кто-то хочет вычислить arcsin (0), ответ может быть 0, 2π (360 °) или -π (-180 °), чтобы назвать несколько вариантов! Все они верны, но обычно мы даем только одно число, называемое основным значением .

Сокращение	Определение	Домен arcsin x для реального результата	Диапазон обычных основных значений
arcsin (x) sin -1 x, asin	х = грех (у)	-1 ≤ х ≤ 1	-π / 2 ≤ y ≤ π / 2 -90 ° ≤ y ≤ 90 °

Arcsin (x) — наиболее распространенное обозначение, так как sin ^-1 x может привести к путанице (потому что sin ^-1 x ≠ 1 / sin (x)).Аббревиатура asin обычно используется в языках программирования.

График arcsin x

Поскольку синус основной функции не является взаимно однозначным, ее область должна быть ограничена, чтобы гарантировать, что арксинус также является функцией. Обычно выбирается область -π / 2 ≤ y ≤ π / 2. Это означает, что диапазон обратной функции будет равен диапазону основной функции; таким образом, диапазон функции arcsin равен [−π / 2, π / 2], а область arcsine находится между [−1,1]. Ниже вы можете найти график arcsin (x), а также некоторые часто используемые значения арксинуса:

x	arcsin (x)		График
	°	рад
-1	-90 °	-π / 2	Geek3, CC BY-SA 4.0 через Wikimedia Commons
-√3 / 2	-60 °	-π / 3
-√2 / 2	-45 °	-π / 4
-1/2	-30 °	-π / 6
0	0 °	0
1/2	30 °	π / 6
√2 / 2	45 °	π / 4
√3 / 2	60 °	π / 3
1	90 °	π / 2

Хотите знать, откуда взялся этот график arcsin x? Его можно найти, отразив график sin (x) в диапазоне [-π / 2 π / 2] через линию y = x:

Jaro.p CC BY-SA 3.0, через Wikimedia Commons

Обратный синус, тригонометрические функции и другие отношения

Связь между тригонометрическими функциями и арксинусом может помочь вам лучше понять тему. Прямоугольный треугольник с гипотенузой длины 1 — хорошая отправная точка.

Напоминаем: для прямоугольного треугольника функция синуса берет угол θ и возвращает отношение противоположности / гипотенузы, которое равно x в нашем примерном треугольнике.Функция обратного синуса, арксинус, принимает отношение противоположности / гипотенузы (x) и возвращает угол θ. Итак, зная, что для нашего треугольника arcsin (x) = θ, мы также можем записать, что:

• Синус: sin (arcsin (x)) = x
• Косинус: cos (arcsin (x)) = √ (1-x²)
• Касательная: tan (arcsin (x)) = x / √ (1-x²)

Другие полезные отношения с арксинусом:

• arcsin (x) = π / 2 - arccos (x)
• arcsin (-x) = -arcsin (x)

Иногда нужны интеграл и производная от arcsin:

• интеграл от arcsin: arcsin (x) dx = x arcsin (x) + √ (1 - x²) + C

• производная от arcsin: d / dx arcsin (x) = 1 / √ (1 - x²) где x ≠ -1, 1

Пример использования калькулятора arcsin

Арксинус — полезная функция e.грамм. в нахождении угла прямоугольного треугольника. Если вы ищете углы в прямоугольном треугольнике и знаете длины сторон, хорошо известная теорема Пифагора не будет столь полезной. Чтобы найти углы прямоугольного треугольника, нужно применить арксинус:

• для α: sin (α) = a / c, поэтому α = arcsin (a / c)
• для β: sin (β) = b / c, поэтому β = arcsin (b / c)

Итак, предположим, что у нас есть два значения, заданные в прямоугольном треугольнике, a = 6 и c = 10, и мы хотели бы найти значение угла α:

1. Введите значение, по которому вы хотите найти арксинус .В нашем случае это 6/10. Таким образом, вы можете ввести значение 0,6, но форма 6/10 также будет работать. Просто помните, что значение должно быть от -1 до 1.
2. И … вот и все! Калькулятор arcsin выполнил свою работу, и вы нашли арксинус своего значения . Теперь вы знаете, что арксинус (6/10) = 36,87 °

Отлично! Теперь, когда вы понимаете, что такое арксинус, может быть, вы захотите познакомиться с более продвинутыми приложениями тригонометрии? Например, закон синусов (тесно связанный с законом косинусов) является обязательным при решении задач треугольника.

Калькулятор Arctan. Найти арктангенс

Воспользуйтесь этим калькулятором арктангенса, чтобы быстро найти арктангенс. Ищете ли вы простой ответ на вопрос «что такое арктан?» или вам интересно узнать об интегральном или производном от arctan, вы попали в нужное место. Ниже вы также найдете график arctan, а также аккуратную таблицу с часто используемыми значениями, такими как arctan (1) и arctan (0). Кроме того, вы можете просто ввести интересующее значение в этот инструмент, и вы найдете ответ в мгновение ока.

Заинтересованы в более продвинутой тригонометрии? Если вам нужно решить треугольники, ознакомьтесь с нашими калькуляторами закона синусов и закона косинусов.

Что такое арктан?

Арктангенс — это функция, обратная касательной. Проще говоря, мы используем arctan, когда хотим найти угол, для которого нам известно значение тангенса.

Однако, в самом строгом смысле, поскольку касательная является периодической тригонометрической функцией, у нее нет обратной функции. Тем не менее, мы можем определить обратную функцию, если ограничим область до интервала, в котором функция является монотонной.Обычно выбираемый интервал -π / 2

рэнд

Сокращение	Определение	Домен арктана x	Диапазон обычных основных значений
arctan (x) tan -1 x, atan	х = загар (у)	все действительные числа	-π / 2 -90 °

Использование соглашения tan ^-1 x может привести к путанице в отношении разницы между арктангенсом и котангенсом.Оказывается, арктан и детская кроватка — это действительно разные вещи:

• cot (x) = 1 / tan (x) , поэтому котангенс в основном является обратной величиной тангенса или, другими словами, мультипликативной обратной величиной
• arctan (x) — это угол, тангенс которого равен x

Надеемся, что теперь вы не сомневаетесь в том, что арктан и котан разные. Чтобы избежать дальнейших недоразумений, вы можете использовать arctan (x), а не tan ^-1 x нотация .

График Arctan

Ограничивая область определения функции главной касательной, мы получаем значение арктангенса, которое изменяется исключительно в диапазоне от −π / 2 до π / 2 радиан.Однако область определения функции арктангенса — это все действительные числа. Тогда график выглядит следующим образом:

График	Обычно используемые значения
	x арктан (х) рад ° -∞ -π / 2 -90 ° -3 -1.2490 -71,565 ° -2 -1,1071 -63,435 ° -√3 -π / 3 -60 ° -1 -π / 4 -45 ° -√3 / 3 -π / 6 -30 ° 0 0 0 ° √3 / 3 π / 6 30 ° 1 π / 4 45 ° √3 π / 3 60 ° 2 1.1071 63,435 ° 3 1,2490 71,565 ° ∞ π / 2 90 °

Как создается этот арктановый граф? Отражая tan (x) в диапазоне (-π / 2 π / 2) через линию y = x.Вы также можете посмотреть на это, как поменять местами горизонтальную и вертикальную оси:

Свойства Arctan, отношения с тригонометрическими функциями, интеграл и производная от arctan

Отношения в тригонометрии имеют решающее значение для более глубокого понимания этой темы. Изучение прямоугольного треугольника с длинами сторон 1 и x является хорошей отправной точкой, если вы хотите найти отношения между arctan и основными тригонометрическими функциями:

• Синус: sin (arctan (x)) = x / √ (1 + x²)
• Косинус: cos (arctan (x)) = 1 / √ (1 + x²)
• Тангенс: tan (arctan (x)) = x

Другие полезные отношения с арктангенсом:

• arctan (x) = π / 2 - arccot ​​(x)
• арктан (-x) = -арктан (x)
• arcsin (x) = arctan (x / √ (1 - x²))
• интеграл от arctan: arctan (x) dx = x arctan (x) - (1/2) ln (1 + x²) + C
• производная от arctan: d / dx arctan (x) = 1 / (1 + x²) где x ≠ -i, i
• arctan (x) + arctan (1 / x) = π / 2 , для x> 0 и arctan (x) + arctan (1 / x) = -π / 2 , для x <0

Первое уравнение легко доказать из свойств прямоугольного треугольника с длинами сторон 1 и x, так как мы прекрасно знаем, что сумма углов в треугольнике равна 180 °.Вычитая прямой угол, равный 90 °, мы получаем два непрямых угла, которые в сумме должны составлять 90 °. Таким образом, мы можем записать углы как arctan (x) и arctan (1 / x).

Калькулятор Arctan — как пользоваться

Это действительно один из самых простых в использовании калькуляторов! Просто введите число, по которому вы хотите найти арктанган . Поскольку домен arctan — это все вещественные числа, вам не о чем беспокоиться. Допустим, мы хотим найти арктангенс 1. Просто введите число, и калькулятор арктангенса отобразит результат .Как мы и ожидали, арктангенс 1 равен 45 °. Этот калькулятор арктангенса работает и в обратном направлении, то есть как стандартный калькулятор тангенса — введите угол во второе поле, и появится тангенс этого угла.

Синус, косинус, тангенс

Три функции, но та же идея.

Прямой треугольник

Синус, косинус и тангенс — основные функции, используемые в тригонометрии, они основаны на прямоугольном треугольнике.

Прежде чем углубляться в функции, полезно присвоить имя каждой стороне прямоугольного треугольника:

• «Противоположно» противоположно углу θ
• «Соседний» примыкает (рядом) к углу θ
• «Гипотенуза» — длинная

Соседний всегда находится рядом с углом

И Напротив находится напротив угла

Синус, косинус и тангенс

Синус , Косинус и Касательная (часто сокращается до sin , cos и tan ), каждая из которых имеет отношение сторон прямоугольного треугольника:

Для заданного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или малый треугольник

Для их расчета:

Разделите длину одной стороны на другую

Пример: Что такое синус 35 °?

Используя этот треугольник (длины до одного десятичного знака):

sin (35 °)	= Напротив Гипотенуза
	= 2.8 4,9
	= 0,57 …
cos (35 °)	= Соседний Гипотенуза
	= 4,0 4,9
	= 0,82 …
желто-коричневый (35 °)	= Напротив Соседний
	= 2.8 4,0
	= 0,70 …

Размер не имеет значения

Треугольник может быть большим или маленьким, и соотношение сторон остается неизменным .

Только угол меняет соотношение.

Попробуйте перетащить точку «A», чтобы изменить угол, и точку «B», чтобы изменить размер:

На хороших калькуляторах есть sin, cos и tan, чтобы облегчить вам задачу.Просто вставьте угол и нажмите кнопку.

Но все же нужно запомнить, что означают !

В форме изображения:

Практика здесь:

Sohcahtoa

Как запомнить? Думайте «Sohcahtoa» !

Работает так:

Soh …	S ine = O pposite / H ypotenuse
…ка …	C осин = A djacent / H ypotenuse
… toa	T angent = O pposite / A djacent

Вы можете узнать больше о sohcahtoa … запомните, это может помочь на экзамене!

Углы от 0 ° до 360 °

Перемещайте мышь, чтобы увидеть, как разные углы (в радианах или градусах) влияют на синус, косинус и тангенс.

На этой анимации гипотенуза равна 1, образуя единичную окружность.

Обратите внимание, что соседняя сторона и противоположная сторона могут быть положительными или отрицательными, что также приводит к изменению синуса, косинуса и тангенса между положительными и отрицательными значениями.

«Почему согрешили, и tan не пошли на вечеринку?» «… всего cos !»

Примеры

Пример: каковы синус, косинус и тангенс 30 °?

Классический треугольник 30 ° имеет гипотенузу длины 2, противоположную сторону длины 1 и смежную сторону √3:

Теперь мы знаем длины, можем вычислить функции:

Синус		sin (30 °) = 1/2 = 0.5
Косинус		cos (30 °) = 1,732 / 2 = 0,866 …
Касательная		тангенс угла (30 °) = 1 / 1,732 = 0,577 …

(возьмите калькулятор и проверьте его!)

Пример: каковы синус, косинус и тангенс угла 45 °?

Классический треугольник 45 ° имеет две стороны 1 и гипотенузу √2:

Синус		sin (45 °) = 1/1.414 = 0,707 …
Косинус		cos (45 °) = 1 / 1,414 = 0,707 …
Касательная		тангенс угла (45 °) = 1/1 = 1

Почему?

Почему эти функции важны?

• Потому что они позволяют нам вычислять углы, когда мы знаем стороны
• И они позволяют нам определять стороны, когда мы знаем углы

Пример: используйте синусоидальную функцию

, чтобы найти «d»

Мы знаем:

• Кабель составляет угол 39 ° относительно морского дна
• Кабель длиной 30 метров .

И мы хотим знать «d» (расстояние вниз).

Начать с: sin 39 ° = противоположно / гипотенуза

sin 39 ° = d / 30

Поменять местами стороны: d / 30 = sin 39 °

С помощью калькулятора найдите sin 39 °: d / 30 = 0,6293 …

Умножаем обе стороны на 30: d = 0,6293… x 30

d = 18,88 с точностью до 2 знаков после запятой.

Глубина «d» 18,88 м

Упражнение

Попробуйте это бумажное упражнение, в котором вы можете вычислить синусоидальную функцию. для всех углов от 0 ° до 360 °, а затем нарисуйте результат.Это поможет вам понять эти относительно простые функции.

Вы также можете увидеть графики синуса, косинуса и тангенса.

И поиграйте с пружиной, создающей синусоидальную волну.

Менее распространенные функции

Чтобы завершить картину, есть еще 3 функции, в которых мы разделяем одну сторону на другую, но они не так часто используются.

Они равны 1, деленному на cos , 1, деленному на sin , и 1, деленному на tan :

Секущая функция:		сек ( θ ) = Гипотенуза Соседний		(= 1 / cos)
Косекансная функция:		csc ( θ ) = Гипотенуза Напротив		(= 1 / sin)
Функция котангенса:		детская кроватка ( θ ) = Соседний Напротив		(= 1 / tan)

Калькулятор тангенса синуса косинуса

— Онлайн калькулятор тангенса косинуса синуса

Тангенс-косинус — основные функции тригонометрии, основанный на прямоугольном треугольнике.

Что такое калькулятор тангенса косинуса синуса?

«Калькулятор синус-косинус-тангенс Cuemath» — это онлайн-инструмент, который помогает вычислять значения синуса, косинуса и тангенса для заданного угла тета. Этот онлайн-калькулятор синус-косинуса и тангенса поможет вам рассчитать значения синуса, косинуса и тангенса для заданного угла тета за несколько секунд.

Как пользоваться калькулятором тангенса синуса и косинуса?

Выполните следующие действия, чтобы найти значения синуса, косинуса и тангенса для заданного угла theta:

• Шаг 1: Выберите из раскрывающегося списка синус, косинус и коэффициент тангенса для заданного угла тета.
• Шаг 2: Введите угол тета (в градусах) в данное поле ввода.
• Шаг 3: Нажмите кнопку «Рассчитать» , чтобы найти значения синуса, косинуса и тангенса для заданного угла тета.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и найти значения синуса, косинуса и тангенса для различных углов.

Как найти коэффициент касания синуса и косинуса?

Синусоидальная функция определяется как отношение длины противоположной стороны к длине гипотенузы в прямоугольном треугольнике.Синус — это тригонометрическая функция угла. Он обозначается как sinθ, где θ — угол между двумя сторонами.

Функция косинуса определяется как отношение длины смежной стороны к длине гипотенузы в прямоугольном треугольнике. Косинус — это тригонометрическая функция угла. Он обозначается как cosθ, где θ — угол между двумя сторонами.

Функция касательной определяется как отношение длины противоположной стороны к длине соседней стороны в прямоугольном треугольнике.Касательная — это тригонометрическая функция угла. Он обозначается как tanθ, где θ — угол между двумя сторонами.

Хотите найти сложные математические решения за секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. С Cuemath находите решения простым и легким способом.

Забронируйте бесплатную пробную версию Класс

1. Пример 1: Найти значение синуса, если θ = 45 °?

   Решение:

   При θ = 45 °

   грех 45 ° = 1 / √2

   = 0.71

2. Пример 2: Найдите значение косинуса, если θ = 60 °?

   Решение:

   При θ = 60 °

   cos 60 ° = 1/2

3. Пример 3: Найти значение тангенса, если θ = 45 °?

   Решение:

   При θ = 45 °

   загар 45 ° = 1

перейти к слайду перейти к слайду

Точно так же вы можете попробовать калькулятор, чтобы найти значения синуса, косинуса и тангенса для следующих значений:

.